Partikelgrößenanalyse mit Laserbeugung
Während der letzten 50 Jahre hat sich die Laserbeugung sowohl in Labor- als auch in Prozessumgebung zum führenden Messprinzip in der Partikelgrößenanalyse aller Arten von Pulvern, Aerosolen, Suspensionen, Emulsionen und Sprays entwickelt.
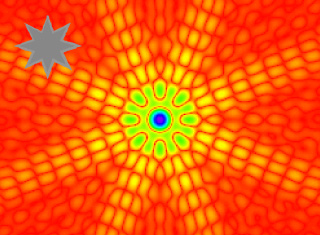
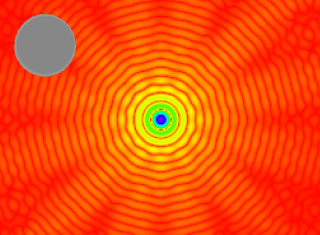
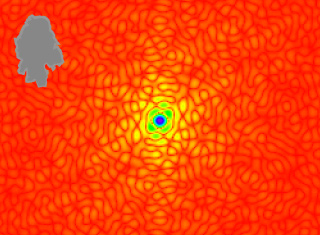
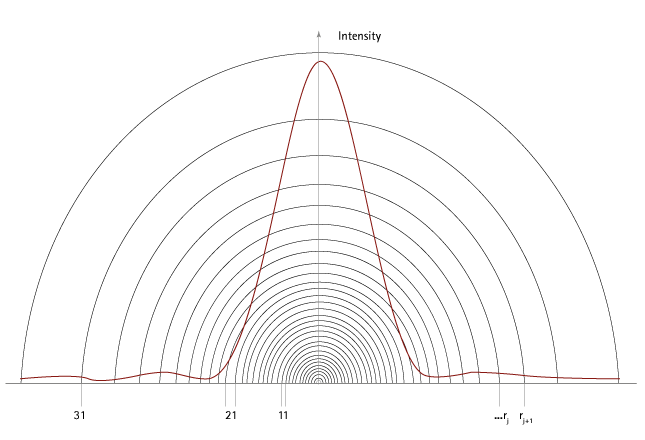
Die Beugung des Laserlichts resultiert aus der Wechselwirkung des Lichts mit den Partikeln und lässt sich mathematisch mit der Fraunhofer- oder der Mie-Theorie beschreiben. Für ein einzelnes sphärisches Partikel zeigt das Beugungsmuster eine typische Ringstruktur. Der Abstand r0 des ersten Intensitätsminimums zum Zentrum ist abhängig von der Partikelgröße, wie aus Abb. 1 und Abb. 2 ersichtlich. Die Aufnahme der Intensitätsverteilung des gebeugten Lichts geschieht gewöhnlich mit Hilfe eines Multielementphotodetektors, wie in Abb. 3 gezeigt.
1 | Beugungsmuster eines großen Partikels
2 | Beugungsmuster eines kleineren Partikels
3 | Intensitätsverteilung eines kleinen Partikels aufgenommen mit einem semizirkularen Photodetektor
Die Streuung von unpolarisiertem Laserlicht an einem einzelnen kugelförmigen Partikel kann mathematisch wie folgt beschrieben werden:
Dabei ist
Ι(θ) die gesamte Streuintensität als Funktion des Winkels θ in Bezug auf die Vorwärtsrichtung
I0 die Beleuchtungsstärke
k der Wellenvektor 2π/λ
a die Entfernung des Streuzentrums zum Detektor und
S1(θ) und S2(θ) sind dimensionslose, komplexwertige Funktionen, die die Änderung der Amplitude des senkrecht und parallel polarisierten Lichts beschreiben.
Verschiedene Algorithmen wurden für die Berechnung von I(θ) entwickelt. Die Lorenz-Mie Theorie basiert auf der Annahme kugelförmiger, isotroper und homogener Partikel, die alle mit einem gemeinsamen komplexen Brechungsindex m = n-ik beschrieben werden können. Der Brechungsindex muss für die Auswertung genau bekannt sein, was in der Praxis insbesondere für den imaginären Anteil k häufig nicht der Fall ist. Eine weitere Herausforderung sind Mischungen aus verschiedensten Komponenten mit unterschiedlichen Brechungsindizes.
Die Fraunhofer-Theorie betrachtet den Teil der Lichtablenkung, der ausschließlich durch Beugung zustande kommt. Ein großer Vorteil besteht darin, dass keine Kenntnisse über den Brechungsindex des untersuchten Materials notwendig sind. I(θ) kann mit dem dimensionslosen Größenparameter α=πx/λ vereinfacht werden (siehe Formel). Diese Theorie beschreibt keine Polarisation und vernachlässigt eine mögliche Lichtdurchlässigkeit von Partikeln.
Maßgabe der Fraunhofer-Beugung ist dabei die Messung absorbierender Partikel innerhalb vergleichsweiser kleiner Winkel in Vorwärtsrichtung. Im Gegensatz zur Mie-Theorie kommt das Fraunhofer-Modell ohne die Kenntnis optischer Konstanten aus. Sie allein ist auch bei Mischungen verschiedener Materialien und Formen anwendbar. Die ermittelte Partikelgröße entspricht dabei dem Äquivalentdurchmesser der beugungsgleichen Kugel.
Die gleichzeitige Beugung an mehr als einem Partikel resultiert in einer Überlagerung der Beugungsmuster der einzelnen Partikel solange die Partikel sich bewegen und sich die Beugung zwischen den Partikeln dabei herausmittelt. Schon 1983 hat Sympatec Pionierarbeit in der Auswertung der Größenverteilung mit einem parameterfreien und modellunabhängigen mathematischen Algorithmus geleistet. Dieses wurde mit der Einführung des Phillips-Twomey-Algorithmus für den inversen Prozess erreicht.
Beugungsmuster von nicht sphärischen Partikeln
Berechnete Beugungsmuster für nicht sphärische Partikel (siehe die grauen Partikelformen in den einzelnen Abbildungen). Alle Beugungsmuster zeigen eine Symmetrie von 180°.
