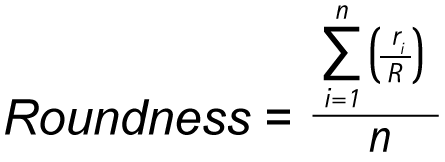Partikelform und Formparameter
Bei den Bildauswertungsverfahren ist die grundlegende Messinformation die Projektionsfläche des Partikels. Dies unterscheidet die Bildauswertung von der Laserbeugung oder der Ultraschallextinktion, denn in der projizierten Fläche ist eine zusätzliche Information über die Partikelform enthalten, wenn auch nur zweidimensional als Kontur der Fläche.
Die beliebig geformte Projektionsfläche eines Partikels kann durch diverse Angaben beschrieben werden, die als Ergebnis jeweils die Partikelgröße definieren. Diese Angaben können sowohl Durchmesser als auch Längenangaben sein, die im Folgenden aber verallgemeinert als Durchmesser bezeichnet werden. Zu ihrer Bestimmung sind zahlreiche Verfahren veröffentlicht worden, von denen die wichtigsten in der QICPIC Auswertesoftware zur Verfügung stehen. Andere Kenngrößen sind die sogenannten Formparameter die zur Beschreibung der Partikelform dienen.
Die Beschreibung von Fasern ist ein relativ junges und stark in Entwicklung befindliches Feld der Bildanalyse. Daher sind weder die Definitionen der Größen- und Formparameter standardisiert noch sind es die Algorithmen zu ihrer Berechnung. PAQXOS bietet die Berechnung der Länge und des Durchmessers einer Faser sowie der Geradheit als Formparameter.
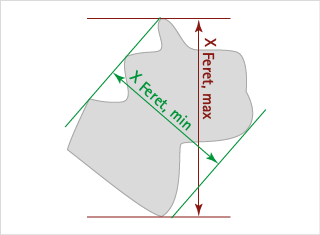
Kein Durchmesser im eigentlichen Sinne, sondern Grundlage für eine Gruppe von Kenngrößen, die alle durch den Abstand zweier Tangenten an die Partikelkontur in einer festgelegten Messrichtung definiert sind. Sinngemäß ist der Feret-Durchmesser das Messergebnis einer Schieblehre (Schieblehrenprinzip). Allgemein wird er als Abstand zwischen zwei parallelen Tangenten eines Partikels in einem beliebigen Winkel beschrieben. In der Praxis werden der Minimum xFmin und Maximum Feret Durchmesser xFmax>, der mittlere Feret Durchmesser und der Feret Durchmesser unter 90° zum Minimum und Maximum Feret Durchmesser xFmax90 verwendet. Der Miniumum Feret Durchmesser wird oft als Äquivalentdurchmesser zur Siebanalyse eingesetzt.
Feret Durchmesser, maximal | FERETmax
Hierzu werden intern die Feret-Durchmesser für eine ausreichende Anzahl von Winkeln ermittelt und der größte Wert ausgewählt. Bei unregelmäßigen Partikeln variiert der Feret-Durchmesser stärker als bei kugelförmigen Partikeln, so dass der maximale Feret-Durchmesser immer über dem Durchmesser des Kreises mit gleicher Projektionsfläche (EQPC) liegt.
Feret Durchmesser, minimal | FERETmin
Hierzu werden intern die Feret-Durchmesser für eine ausreichende Anzahl von Winkeln ermittelt und der kleinste Wert ausgewählt. Bei unregelmäßigen Partikeln variiert der Feret-Durchmesser stärker als bei kugelförmigen Partikeln, so dass der minimale Feret-Durchmesser immer unter dem Durchmesser des Kreises mit gleicher Projektionsfläche (EQPC) liegt.
Mittelwert der Feret-Durchmesser über alle Messrichtungen nach dem oben beschriebenen Prinzip.
Zunächst wird der maximale Feret-Durchmesser FERETmax bestimmt. Ausgegeben wird der Feret-Durchmesser, der um einen Winkel von 90 Grad zu diesem maximalen Feret-Durchmesser versetzt liegt.
Zunächst wird der minimale Feret-Durchmesser FERETmin bestimmt. Ausgegeben wird der Feret-Durchmesser, der um einen Winkel von 90 Grad zu diesem minimalen Feret-Durchmesser versetzt liegt.
Der Zylindervolumen Feret-Durchmesser FERETvol gibt den Durchmesser einer Kugel wieder, die das gleiche Volumen hat wie ein Zylindermit dem Durchmesser FERETmin und der Länge FERETmax.
Die Berechnung des umschließenden Rechtecks mit der geringsten Fläche beruht auf dem Produkt des Feret-Durchmessers FERETmax mit seinem Pendant in dazu senkrechter Richtung FERETmax90 für ein Partikel. Die Länge dieses Rechtecks wird als BRmax und seine Breite als BRmin ausgegeben.
Kleinstes begrenzendes Rechteck, Länge / BRmax
Die längere Kante des umschließenden Rechtecks mit der kleinsten Fläche wird ausgegeben.
Kleinstes begrenzendes Rechteck, Breite / BRmin
Die kürzere Kante des umschließenden Rechtecks mit der kleinsten Fläche wird ausgegeben. Dieser Wert korrespondiert recht gut mit dem Ergebnis einer Siebanalyse.
Als Sehnenlänge wird der Abstand zweier Konturpunkte definiert. Die Berechnung erfolgt in zwei Schritten und liefert zwei Angaben zu Sehnenlängen.
Das Abbild eines Partikels wird um 180 Grad in Schritten von jeweils 9 Grad rotiert. Zu jeder Orientierung des Partikels wird dann die maximale horizontale Sehnenlänge bestimmt. Das folgende Bild zeigt die Skizze eines Partikels für 6 ausgewählte Orientierungen, mit den jeweils maximalen, horizontalen Sehnen.
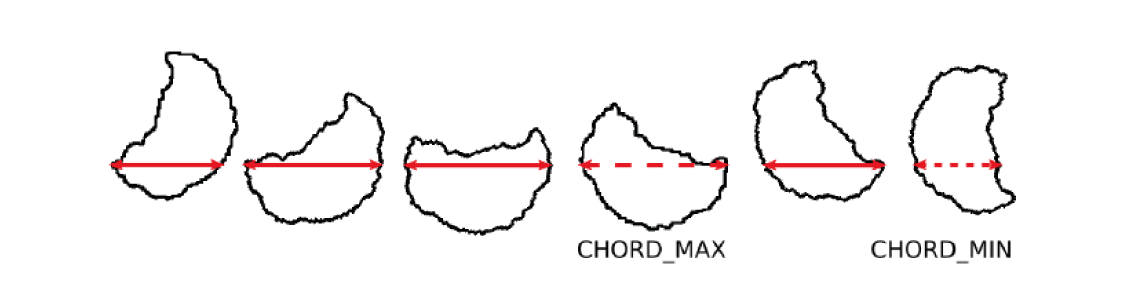
Aus den berechneten Sehnenlängen ergeben die längste maximale Sehnenlänge CHORDmax und die kürzeste maximale Sehnenlänge CHORDmin die beiden Ergebnisse.
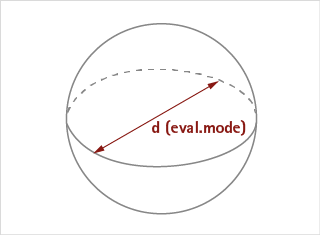
Kugelvolumen aus dem aktuellen Standarddurchmesser
Bei diesem Model wird das Volumen immer mit dem ausgewählten Standarddurchmesser berechnet.
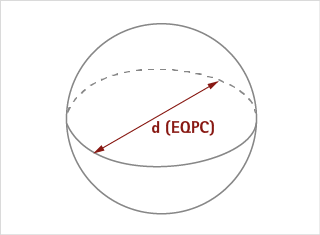
Kugelvolumen aus EQPC
Bei diesem Model wird das Volumen der Kugel immer mit dem EQPC Durchmesser des Partikels berechnet, unabhängig vom ausgewählten Standarddurchmesser.
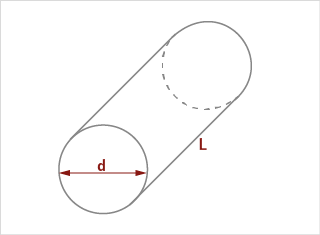
Zylindervolumen
Zwei unterschiedliche Zylindervolumenmodelle
A) FERET Zylinder
d = FERETmin | L = FERETmax
B) Faserlänge und Faserbreite
d = DIFI | L = LEFI
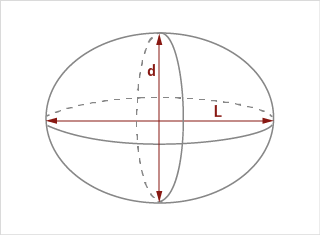
Ellipsoidvolumen
Zwei unterschiedliche Arten zur Berechnung des Ellipsoids:
A) FERET Ellipsoid
d = FERETmin | L = FERETmax
B) CHORD Ellipsoid
d = CHORDmin | L = CHORDmax
Seitenverhältnis
Der Unterschied des maximalen zum minimalen Feret-Durchmesser ein weiteres Maß für die Beurteilung der Partikelform (Engl. Stichwort: aspect ratio). Das Seitenverhältnis ψA (0 < ψA≤ 1) ergibt sich aus dem Verhältnis vom Minimum zum Maximum Feret Durchmesser ψA = xFeret min / xFeret max. Es gibt einen Hinweis auf die Ausdehnung des Partikels. Manchmal findet man in der Literatur auch 1/ψA als Definition für die Sphärizität.
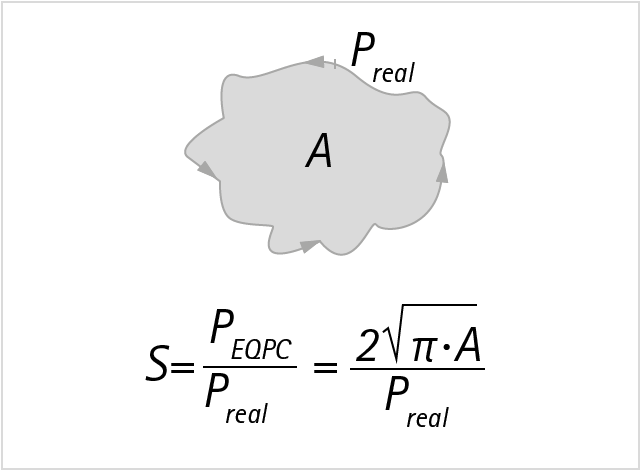
Sphärizität
Die Sphärizität S (Kugelförmigkeit) ist das Verhältnis des Umfangs des flächengleichen Kreises PEQPC, zum tatsächlichen Umfang, Preal. Das Ergebnis ist ein Wert zwischen 0 und 1. Je kleiner der Wert ist, desto unregelmäßiger ist das Partikel geformt. Dies ist die Konsequenz aus der Tatsache, dass sich eine unregelmäßige Partikelform in einem vergrößerten Umfang zeigt. Verglichen wird grundsätzlich mit dem flächengleichen Kreis, da dieser den kleinsten aller möglichen Umfänge für eine Projektionsfläche der Größe A aufweist.
Elongation

Die Elongation ist das Verhältnis von Durchmesser und Länge einer Faser, entsprechend der Formel DIFI / LEFI. Dieser Parameter wird auch Exzentrizität genannt.
Konvexität
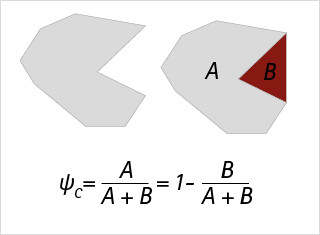
Die Konvexität ist ein wichtiger Formparameter, der die Kompaktheit eines Partikels beschreibt. Das nachfolgende Bild zeigt ein Partikel mit Projektionsfläche A (grau/hell), die auf der rechten Seite ein konkaves Gebiet der Fläche B (rot/dunkel) frei lässt. Der theoretische Maximalwert ist 1, d.h. wenn es keine konkaven Bereiche gibt. Bedingt durch das Detektordesign einer Digitalkamera (quadratische Bildpunkte), scheinen alle Partikel kleine konkave Bereiche aufzuweisen, die den winzigen Stufen an jedem Bildpunkt der Umfangslinie entsprechen. Daher ist die größte real berechnete Konvexität meist auf 0,99 begrenzt.
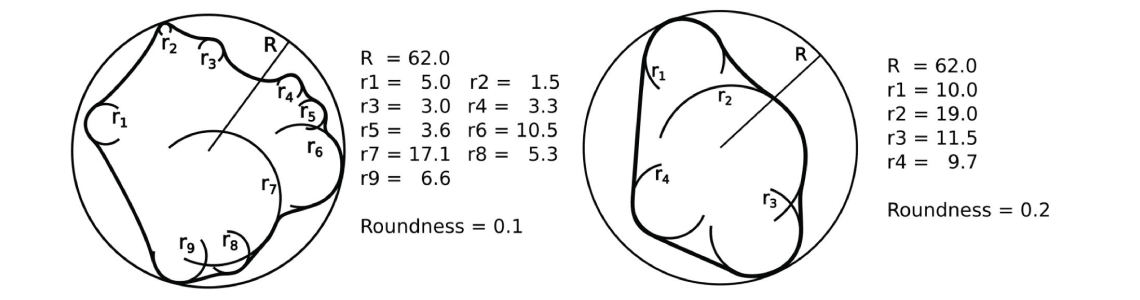
Rundheit
Geradheit für faserförmige Partikel
Die meisten Fasern, besonders längere, neigen zum Zusammenrollen, und es hat die unterschiedlichsten Ansätze gegeben, dieses Phänomen durch einen einzigen Parameter zu beschreiben. Eine der möglichen Definitionen ist die Geradheit (engl. straightness), gemäß ISO Norm 9276-6:
STRAIGHTNESS = FERETmax / LEFI Die Definitionen für LEFI und FERETmax
sind oben in diesem Kapitel zu finden. Ein Wert von 1 für die Geradheit stellt ein vollkommen gerades Partikel dar, während Werte nahe Null für stark gekrümmte Partikel (eingerollte Fasern) stehen. Eine ältere Definition der Geradheit ist der Curl Index:
CURLindex = LEFI / FERETmax - 1
womit die Tradition in einigen Industriebranchen, vor allem der Holzverarbeitung, abgebildet wurde.
Ein faserförmiges Partikel zeichnet sich aus durch eine Länge, die typischerweise viel größer ist als ihr Durchmesser und eine unregelmäßige Form. Folglich werden sowohl die Länge als auch der Durchmesser zur korrekten Beschreibung einer Faser benötigt.
Obige Definition ist unscharf, aber es gibt keine genauere und somit auch keine standardisiertes Kriterium, welche Partikelform als faserförmig anzusehen ist und welche nicht. Die nachfolgend beschriebenen Auswertemethoden können wahlweise auf Partikel beliebiger Form angewendet werden. Es obliegt dann dem Benutzer, die Verwertbarkeit der erhaltenen Ergebnisse zu beurteilen.
Faserlänge / LEFI
Die Länge einer Faser ist definiert als die direkte Verbindung zwischen ihren entgegengesetzten Enden, somit der längsten direkte Weg von einem Ende zu einem anderen innerhalb der Partikelkontur. Direkt bedeutet ohne Schleifen oder Umwege. Eine Technik, die bei der Berechnung dieses Wertes angewendet wird, heißt "Skelettierung" und bedeutet, dass die Abmessungen der Faser von allen Richtungen so lange reduziert werden bis eine oder mehrere Linien bleiben, die einen Bildpunkt breit sind. Die schwarze Linie in den nachfolgenden Faserbildern stellt den längsten direkten Weg entlang ihres Skeletts dar. Seine Länge ist das Ergebnis der LEFI Berechnung.
Eine sehr einfache Kontur einer Faser ist in Bild 1 dargestellt. Sie ist einfach, weil sie keine Verzweigungen oder Schlaufen hat und das Verhältnis von Länge zu Durchmesser groß ist.
Die Sache wird ein wenig komplizierter für Bild 2. Der Algorithmus zur Identifizierung der entgegengesetzten Enden muss zwei Zweige untersuchen und den längeren auswählen.
Bild 3 zeigt eine komplexe Faser mit Verzweigungen und Schlaufen. Der Effekt des Skelettierungsalgorithmus kann im Bild deutlich erkannt werden. Das Entscheidende für den Algorithmus zur Wegbestimmung ist die Vermeidung von Schlaufen.
Faserdurchmesser / DIFI and DIFIX
Es sind viele Arten vorstellbar, um den Durchmesser einer Faser (DIameter of FIbre) mit einem einzigen Mittelwert zu beschreiben. Die in unserer Software PAQXOS implementierte Methode für das QICPIC Bildanalysesystem ist die Division der Projektionsfläche durch die addierte Länge aller Zweige der Faser.
Die Berechnung von DIFI wird nur auf Fasern angewendet, die vollständig im Bild sind, während DIFIX auch diejenigen Fasern berücksichtigt, die den Bildrand berühren.
Volumenbasierender Faserdurchmesser / VBFD
Dieser Durchmesser ist definiert als Durchmesser einer Kugel mit gleichem Volumen wie die betreffende Faser. Er wird wie folgt berechnet: mit xD, dem Faserdurchmesser (DIFI) und xL, der Faserlänge (LEFI). Der Volumenbasierende Faserdurchmesser ist sehr nützlich für Mischungen aus Granulat und Fasern, bei denen ein Diagramm der Volumenverteilung über der Partikelgröße gewünscht ist. Weder LEFI noch DIFI sind für die x-Achse eines Volumenverteilungsdiagramms geeignet, nur VBFD ermöglicht eine informative Darstellung.